Single Pentode Wien Bridge Oscillator
The oscillator was designed to utilize resistors and capacitors instead of large low-frequency LC tank circuits for generating audio frequencies. It achieved low distortion (less than 0.5%) by employing a two-stage amplifier with sufficient negative feedback to set the gain to exactly 3, which is necessary for the oscillation of the Wien Bridge circuit. A light bulb was incorporated as an amplitude detector and a linear gain-setting resistor for the feedback amplifier. Hewlett acknowledged L. A. Meacham for introducing the light bulb for automatic oscillator gain stabilization, as published in the Bell System Technical Journal, Vol 17, p. 574, October 1938. The Wien Bridge network, invented by Max Wien in 1891, is depicted in this excerpt from Hewlett's thesis, showing half the bridge. At the resonant frequency with equal resistors and capacitors, the attenuation is one-third of the input voltage with zero phase shift. This implies that if a precise gain of 3 can be maintained from the output of the network to the input, a sinusoidal oscillator is established. The simplified circuit illustration indicates the lamp that stabilizes the non-inverting gain of the feedback amplifier to exactly 3x. The resistance of the lamp increases with larger signals applied to it, which means that if oscillations become too large, the lamp's resistance increases, thereby reducing the oscillation amplitude until a stable equilibrium is achieved. At this equilibrium point, the RC-CR Wien network enforces a gain of 3x at the feedback amplifier, effectively adjusting the lamp resistance to yield an amplifier gain of 3x. Consequently, the lamp regulates the oscillation amplitude of the Wien network. This lamp-stabilized Wien Bridge oscillator fundamentally differs from RF LC oscillators typically used in radio circuits, as the oscillation currents and voltages in the Wien oscillator remain nearly perfectly sinusoidal. In contrast, typical RF oscillators with an LC tank circuit exhibit a pure sine wave voltage across the tank circuit, but the oscillations are stimulated by highly non-linear current pulses in a class C regime. The high quality factor (Q > 100) of the LC tank circuit imparts a degree of immunity to variations in the strength of the current pulses driving the oscillations. The amplitude of these class C RF oscillators is controlled either by the self-limiting nature of the current pulses or by localized automatic gain control (AGC) action on these current pulses. The Wien Bridge circuit, characterized by a very low Q, does not exhibit the same behavior. If a class C amplifier were employed instead of a linear amplifier with a gain of 3, the oscillation frequency would depend not only on the RC-CR network time constants but also on the limiting characteristics of the class C amplifier. Therefore, it is crucial that the gain-of-3 amplifier be a highly linear amplifier to ensure that the RC-CR network time constants solely determine the oscillation frequency. One limitation of the Wien Bridge oscillator is its requirement for a non-inverting gain amplifier, which during the tube era typically necessitated a cascade of two inverting stages. This often made the phase-shift oscillator, which requires an inverting gain, a viable alternative for single-tube RC oscillator designs. However, phase-shift oscillators typically require four or more RC pairs to achieve the necessary 180-degree phase shift. The non-inverting voltage gain achievable between the suppressor grid (G3) and the screen grid (G2) in a dual control pentode can be utilized to construct a Wien Bridge oscillator using a single pentode. The following schematic illustrates the 6AS6 dual control pentode functioning as the linear gain-controlled amplifier with a gain of 3 from the suppressor grid G3 at pin 7 to the screen grid G2 at pin 6. The precise gain of 3 from G3 to G2 is automatically regulated by the DC bias at the control grid.
The Wien Bridge oscillator is a critical component in audio frequency generation, relying on the principles of feedback and stability. The fundamental operation revolves around the balance of resistive and capacitive elements that define the oscillation frequency. The use of a two-stage amplifier with negative feedback is essential to maintain the desired gain while minimizing distortion. The inclusion of a light bulb as an amplitude stabilizer is a novel approach that allows for automatic adjustment of gain, ensuring that the output remains stable under varying conditions.
In practical applications, the Wien Bridge oscillator is favored for its ability to produce low-distortion sine waves, making it suitable for audio testing and generation. The design's reliance on linear amplification is crucial, as non-linear amplifiers would introduce unwanted harmonics and distortion. The careful selection of components, including the dual control pentode, ensures that the system can achieve the necessary gain without compromising the integrity of the oscillation.
Moreover, the Wien Bridge oscillator's low Q factor results in a more stable and predictable output compared to RF LC oscillators. This stability is particularly advantageous in audio applications where signal fidelity is paramount. The oscillator's design can be adapted for various frequency ranges by selecting appropriate resistor and capacitor values, providing versatility in its usage.
In summary, the Wien Bridge oscillator represents a sophisticated solution for audio frequency generation, characterized by its low distortion, stability, and innovative use of components such as the light bulb for gain stabilization. Its design principles and operational characteristics make it a valuable tool in the field of electronics, particularly in audio engineering and signal processing.His oscillator sought to use resistors and capacitors instead of bulky low frequency LC tank circuits to generate audio frequencies. He obtained low distortion (<0. 5%) with the use of a two stage amplifier with enough negative feedback to set it`s gain to just 3, as required for oscillation of the Wien Bridge circuit.
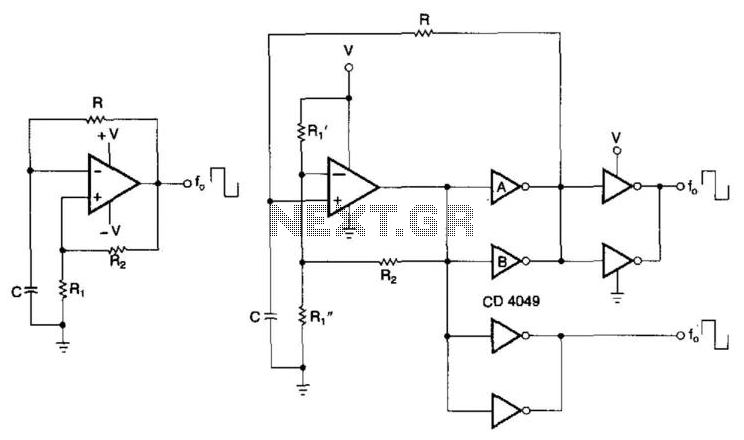
He used a light bulb to serve as amplitude detector and linear gain setting resistor for the fed-back amplifier . Hewlett credits L. A. Meacham with the use of the light bulb for automatic oscillator gain stabilization as published in the Bell System Technical Journal Vol 17, p. 574, 0ctober 1938. The Wien Bridge network was invented by Max Wien in 1891. This excerpt from Hewlett`s thesis shows half the bridge. At the resonant frequency with equal resistors and capacitors, the attenuation is 1/3 of the input voltage with zero phase shift.
This means that if an exact gain of 3 can be provided from the output of the network to the input, we have a sinusoidal oscillator. The simplified circuit on the right shows the lamp that stabilizes the non-inverting gain of the fed-back amplifier to exactly 3x.
The lamp resistance increases when a larger signal is applied to it. This means that if oscillations grow too large, the lamp resistance increases to reduce oscillation amplitude until a stable equilibrium is reached. At this equilibrium point, the RC-CR Wien network forces a gain of 3x at the fed-back amplifier, which is to say, it forces the lamp resistance to a value that yields an amplifier gain of 3x.
In turn, the Lamp forces the Wien network oscillation amplitude. This lamp stabilized Wien bridge oscillator differs fundamentally from RF LC oscillators commonly used in Radio circuits in that the oscillation currents and voltages in the Wien oscillator always remain nearly perfectly sinusoidal. Typical RF oscillators with an LC tank circuit have a very pure sine wave voltage across the the tank circuit, but the oscillations are stimulated with very non-linear current pulses in a class C regime.
The high Q>100 of the LC tank circuit gives the Frequency of these RF oscillators a fair immunity from variations in the strength of the current pulses that stimulate the oscillations. The amplitude of these Class C RF oscillators is controlled by the self limitation of the current pulses or by localized AGC action on these current pulses.
As the plot above shows, the Wien bridge circuit has a very low Q. If a class C amplifier were used instead of the linear amplifier with a gain of 3, the oscillation frequency would be not only a function of the RC-CR network time constants, but also a function of the class C amplifier limiting characteristics. It is essential then that the gain-of-3 amplifier be a very linear amplifier to let the RC-CR network time constants be the sole determinants of the oscillation frequency.
One inconvenience of the Wien bridge oscillator is that it requires a non-inverting gain amplifier, which, in the tube era generally meant a cascade of two inverting stages. This often made the phase shift oscillator which requires an inverting gain, a good alternative for a single tube RC oscillator design.
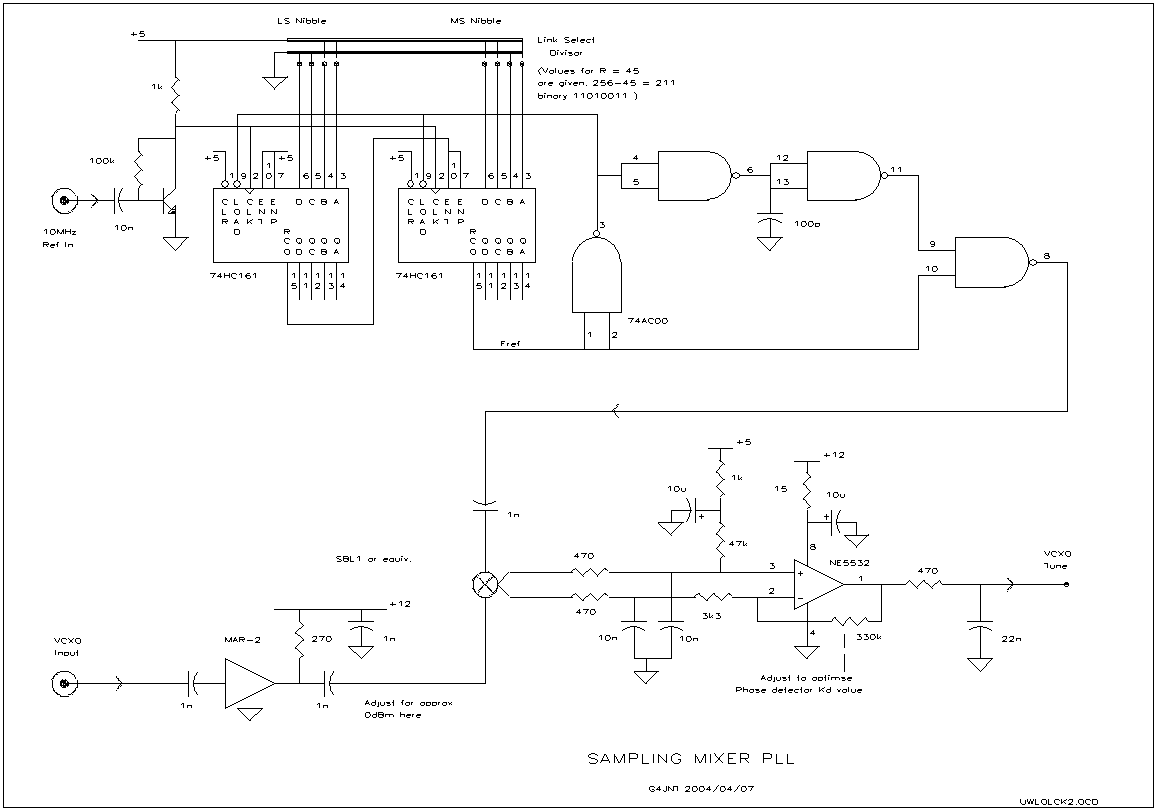
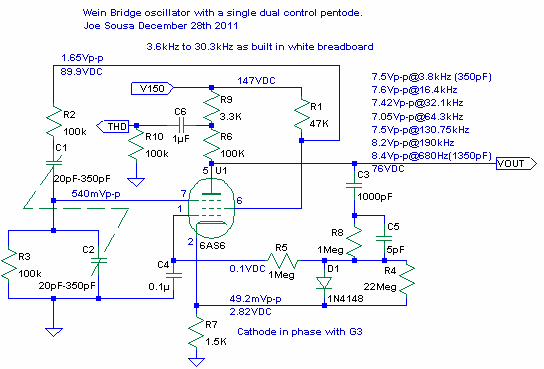
But Phase-shift oscillators require typically 4 or more RC pairs to obtain the 180o phase shift. The non-inverting voltage gain that is possible between the suppressor grid G3 and the screen grid G2 in a dual control Pentode can be used to build a Wien Bridge oscillator with a single Pentode. The following schematic shows the 6AS6 dual control pentode serving as the linear gain controlled amplifier with a gain of 3 from the suppressor grid G3 at pin 7 to the screen grid G2 at pin 6.
The exact gain of 3 from G3 to G2 is controlled automatically with the DC bias at the control grid 🔗 External reference
The Wien Bridge oscillator is a critical component in audio frequency generation, relying on the principles of feedback and stability. The fundamental operation revolves around the balance of resistive and capacitive elements that define the oscillation frequency. The use of a two-stage amplifier with negative feedback is essential to maintain the desired gain while minimizing distortion. The inclusion of a light bulb as an amplitude stabilizer is a novel approach that allows for automatic adjustment of gain, ensuring that the output remains stable under varying conditions.
In practical applications, the Wien Bridge oscillator is favored for its ability to produce low-distortion sine waves, making it suitable for audio testing and generation. The design's reliance on linear amplification is crucial, as non-linear amplifiers would introduce unwanted harmonics and distortion. The careful selection of components, including the dual control pentode, ensures that the system can achieve the necessary gain without compromising the integrity of the oscillation.
Moreover, the Wien Bridge oscillator's low Q factor results in a more stable and predictable output compared to RF LC oscillators. This stability is particularly advantageous in audio applications where signal fidelity is paramount. The oscillator's design can be adapted for various frequency ranges by selecting appropriate resistor and capacitor values, providing versatility in its usage.
In summary, the Wien Bridge oscillator represents a sophisticated solution for audio frequency generation, characterized by its low distortion, stability, and innovative use of components such as the light bulb for gain stabilization. Its design principles and operational characteristics make it a valuable tool in the field of electronics, particularly in audio engineering and signal processing.His oscillator sought to use resistors and capacitors instead of bulky low frequency LC tank circuits to generate audio frequencies. He obtained low distortion (<0. 5%) with the use of a two stage amplifier with enough negative feedback to set it`s gain to just 3, as required for oscillation of the Wien Bridge circuit.
He used a light bulb to serve as amplitude detector and linear gain setting resistor for the fed-back amplifier . Hewlett credits L. A. Meacham with the use of the light bulb for automatic oscillator gain stabilization as published in the Bell System Technical Journal Vol 17, p. 574, 0ctober 1938. The Wien Bridge network was invented by Max Wien in 1891. This excerpt from Hewlett`s thesis shows half the bridge. At the resonant frequency with equal resistors and capacitors, the attenuation is 1/3 of the input voltage with zero phase shift.
This means that if an exact gain of 3 can be provided from the output of the network to the input, we have a sinusoidal oscillator. The simplified circuit on the right shows the lamp that stabilizes the non-inverting gain of the fed-back amplifier to exactly 3x.
The lamp resistance increases when a larger signal is applied to it. This means that if oscillations grow too large, the lamp resistance increases to reduce oscillation amplitude until a stable equilibrium is reached. At this equilibrium point, the RC-CR Wien network forces a gain of 3x at the fed-back amplifier, which is to say, it forces the lamp resistance to a value that yields an amplifier gain of 3x.
In turn, the Lamp forces the Wien network oscillation amplitude. This lamp stabilized Wien bridge oscillator differs fundamentally from RF LC oscillators commonly used in Radio circuits in that the oscillation currents and voltages in the Wien oscillator always remain nearly perfectly sinusoidal. Typical RF oscillators with an LC tank circuit have a very pure sine wave voltage across the the tank circuit, but the oscillations are stimulated with very non-linear current pulses in a class C regime.
The high Q>100 of the LC tank circuit gives the Frequency of these RF oscillators a fair immunity from variations in the strength of the current pulses that stimulate the oscillations. The amplitude of these Class C RF oscillators is controlled by the self limitation of the current pulses or by localized AGC action on these current pulses.
As the plot above shows, the Wien bridge circuit has a very low Q. If a class C amplifier were used instead of the linear amplifier with a gain of 3, the oscillation frequency would be not only a function of the RC-CR network time constants, but also a function of the class C amplifier limiting characteristics. It is essential then that the gain-of-3 amplifier be a very linear amplifier to let the RC-CR network time constants be the sole determinants of the oscillation frequency.
One inconvenience of the Wien bridge oscillator is that it requires a non-inverting gain amplifier, which, in the tube era generally meant a cascade of two inverting stages. This often made the phase shift oscillator which requires an inverting gain, a good alternative for a single tube RC oscillator design.
But Phase-shift oscillators require typically 4 or more RC pairs to obtain the 180o phase shift. The non-inverting voltage gain that is possible between the suppressor grid G3 and the screen grid G2 in a dual control Pentode can be used to build a Wien Bridge oscillator with a single Pentode. The following schematic shows the 6AS6 dual control pentode serving as the linear gain controlled amplifier with a gain of 3 from the suppressor grid G3 at pin 7 to the screen grid G2 at pin 6.
The exact gain of 3 from G3 to G2 is controlled automatically with the DC bias at the control grid 🔗 External reference
Related Circuits
The circuit depicted is a single-phase bridge rectifier. It consists of arms with a cathode (negative electrode) and parallel anodes (positive electrodes) arranged in a configuration that connects multiple rectifier modules to form a bridge, commonly referred to as...
The BTS412B functions as two high-side power MOSFET switches, while two BU271L (50V, Zhang 1n) serve as low-side switches, forming a bi-directional H-bridge DC motor drive circuit. This configuration is designed for electrical automatic door systems, capable of handling...
This circuit is a conventional Pierce type oscillator that utilizes a JFET. It employs fundamental mode crystals and demonstrates good performance and reliability when a low noise JFET is used. The feedback is regulated by the capacitance C1, which...
The emergence of modern radio and radar systems has created a demand for stable harmonic oscillations at specific carrier frequencies to facilitate the necessary modulation and mixing conditions. While early carrier frequencies primarily operated in the low to mid...
A simple FM transmitter connects a home entertainment system to a portable radio that can be moved around the house and into the backyard. For instance, music can be played from a CD player in the living room and...
A schematic for an H-bridge circuit is required to convert a 350V DC input into a 230V AC output at a frequency of 50Hz. The design should utilize a 555 timer integrated circuit (IC) along with MOSFETs. An H-bridge is...