Types of feedback oscillators
This article explains the construction and working of feedback oscillators, with a detailed description of the Wien bridge oscillator and phase shift oscillator, along with their circuit diagrams, basic components, and practical applications. Oscillators are electronic devices that produce a sinusoidal waveform at their output upon the application of DC voltage at their input terminals. Although other types of waveforms can also be generated, the primary waveform produced is sinusoidal. Different types of oscillators exist, including feedback oscillators and negative feedback oscillators. This discussion focuses on classifying feedback oscillators and their working principles. These oscillators utilize resistors and capacitors in their circuitry to provide the necessary feedback to the amplifier. Feedback oscillators can be classified into two main types. One significant type is the feedback circuit that serves as a standard variable frequency testing circuit within the audio frequency range. The operation of this circuit is straightforward and less complex than LC oscillators. It functions as an audio oscillator, typically generating frequencies within the audible range, which are often used in speakers. While sinusoidal waveforms are primarily produced, other waveforms, such as square waves, can also be generated using similar principles. The amplitude generated typically ranges around 25V, with frequencies spanning from 20Hz to 20kHz. The output impedance of the audio oscillator falls between 75 to 600 ohms. The most common oscillators include the Wien bridge oscillator and the phase shift oscillator, both of which utilize RC networks in their operation. Important features of RC oscillators include the Wien bridge's role in providing phase inversion. This phase inversion does not solely imply a 180-degree shift; it can occur at any angle. The Wien bridge operates as an AC bridge, achieving balance at a specific frequency within a given range. A circuit diagram illustrating the circuitry of a Wien bridge network typically includes capacitors, resistors, and an operational amplifier represented by a triangular symbol, receiving input from the network formed by passive components. Conditions for oscillation include that the phase shift between E1 and E2 must equal zero, which is achievable when the bridge is balanced. The frequency of oscillation is determined by specific parameters. Additionally, for oscillations to occur, the product of the amplifier's gain constant and constant H must exceed unity. The bridge must provide feedback to the operational amplifier, ensuring that the value of E2 remains greater than one while the phase shift between E1 and E2 remains zero. It is evident that the frequency of oscillation corresponds to the resonance frequency, and Ea does not equal E1 at any frequency other than the resonance frequency. This results in the difference between Ea and Eb being in phase with E1. The capacitor in the circuit is typically an air variable capacitor mounted on the same shaft, allowing frequency adjustments through this capacitor. However, this method leads to only minor frequency variations, while larger variations require alternative approaches.
The Wien bridge oscillator is a popular feedback oscillator known for its simplicity and effectiveness in generating sinusoidal waveforms. The basic configuration includes a combination of resistors and capacitors arranged in a bridge circuit, with an operational amplifier providing the necessary gain. The Wien bridge employs a specific arrangement of resistors (R1, R2) and capacitors (C1, C2) to establish a feedback loop that maintains oscillation. The balance condition of the bridge, achieved when the gain of the amplifier equals the attenuation of the feedback network, is crucial for sustained oscillation.
The frequency of oscillation (f) can be calculated using the formula:
\[ f = \frac{1}{2\pi R C} \]
where R is the resistance and C is the capacitance in the feedback loop. The operational amplifier must have a gain that compensates for any losses in the bridge circuit to ensure that the overall gain is greater than one. The phase shift introduced by the RC network is vital, as it allows the feedback to reinforce the input signal at the desired frequency, thus generating a stable sinusoidal output.
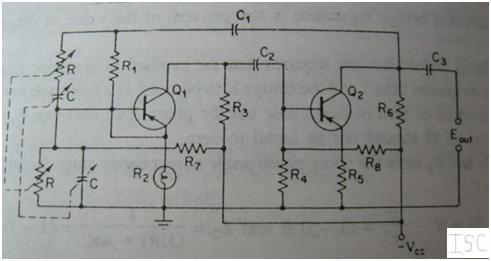
In practical applications, the Wien bridge oscillator is widely used in audio frequency generation, signal processing, and testing equipment, owing to its ability to produce clean and stable waveforms. The phase shift oscillator, on the other hand, utilizes multiple RC stages to achieve a total phase shift of 360 degrees, allowing for oscillation at lower frequencies. Both oscillators demonstrate the essential principles of feedback and phase relationships in electronic circuit design, making them fundamental components in various electronic systems.This article explains the construction and working of feedback oscillators with detailed description of Wien`s bridge oscillator and phase shift oscillator along with their circuit diagram, basic components and practical application Oscillators are those electronic devices that produce a sinusoidal wave form at their output upon application of dc voltage at their input terminals. Although other types of wave forms can also be obtained from them but the basis wave form that they produce is sinusoidal. There can be different types of oscillators like feedback oscillator and negative feedback oscillator.
Here we will be see how we can classify feedback oscillator along with their working principle. These are the oscillators that involve resistor and capacitor in their circuitry for the purpose of required feedback to the amplifier. These categories can further be classified in to two types that are given as: It is so important type of feedback circuit that it provides a standard as the variable frequency testing circuit in audio frequency range.
The operation of this circuit is very simple. Also it is less complex than LC oscillators. It is actually an audio oscillator that is used in the frequency range of audible range generally generated through speakers. And it is seldom used in testing of those electronic circuits that operate upon audio frequencies. Usually a sinusoidal wave form is generated by this type of oscillator that occurs to be variable both in frequency and amplitude so that it may be adjusted according to the concerned application.
Other than sinusoidal waveform some other wave forms can also be generated with help of them like square wave but it utilizes the same principle for that purpose too. The amplitude generated by them is generally in the range of about 25V and frequency occurs in range of about 20Hz to 20 KHz.
The output impedance of the audio oscillator is in the range of 75 to 600 ohm. The most common oscillators as Wien`s bridge oscillator and phase shift oscillator and both of them apply RC network in their operation. There are some very important features regarding RC oscillators are: It is actually a type of feedback oscillator where the function of the Wien`s bridge is to provide inversion of phase.
There inversion of phase does not mean to shift the phase by 180 degree only but the shift in phase can be by any angle. It is basically an AC bridge such the balance is achieves at the particular frequency of the whole frequency under given range.
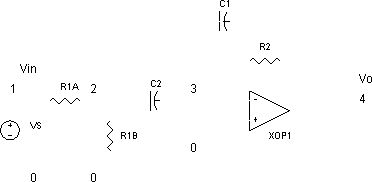
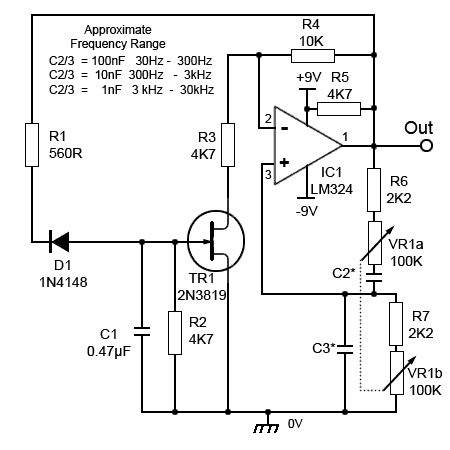
Here is a circuit diagram that shows the circuitry set of a Wien`s bridge network. There are capacitors, resistors and an operational amplifier represented by a triangular symbol getting input from the net work formed by passive components. There are some conditions for oscillations to occur one of them is that he phase shift between E1 and E2 should be equal to zero which is possible in one situation when the bridge is made to be balanced.
The frequency of oscillations is given by: Second condition for making oscillations to occur is the product of gain constant of amplifier and constant H should come to be greater than unity. The requirement of the bridge is to provide feedback to the operational amplifier so the value of E2 should remain always greater than one and phase shift between the two i.
e. E1 and E2 remain to be zero. From the discussion so far it has become clear that frequency of oscillation `s` is equal to that of resonance. And Ea does not come to be equal to E1 at any frequency other than resonance frequency. This results in the consequence that the difference of Ea and Eb does come to be in phase with E1. The capacitor that is used in above circuit is of air by variable capacitor which is mounted on the same shaft.
The change is frequency of the bridge is done by means of this capacitor. But this leads to only small variations in frequency while for large variations there exit 🔗 External reference
The Wien bridge oscillator is a popular feedback oscillator known for its simplicity and effectiveness in generating sinusoidal waveforms. The basic configuration includes a combination of resistors and capacitors arranged in a bridge circuit, with an operational amplifier providing the necessary gain. The Wien bridge employs a specific arrangement of resistors (R1, R2) and capacitors (C1, C2) to establish a feedback loop that maintains oscillation. The balance condition of the bridge, achieved when the gain of the amplifier equals the attenuation of the feedback network, is crucial for sustained oscillation.
The frequency of oscillation (f) can be calculated using the formula:
\[ f = \frac{1}{2\pi R C} \]
where R is the resistance and C is the capacitance in the feedback loop. The operational amplifier must have a gain that compensates for any losses in the bridge circuit to ensure that the overall gain is greater than one. The phase shift introduced by the RC network is vital, as it allows the feedback to reinforce the input signal at the desired frequency, thus generating a stable sinusoidal output.
In practical applications, the Wien bridge oscillator is widely used in audio frequency generation, signal processing, and testing equipment, owing to its ability to produce clean and stable waveforms. The phase shift oscillator, on the other hand, utilizes multiple RC stages to achieve a total phase shift of 360 degrees, allowing for oscillation at lower frequencies. Both oscillators demonstrate the essential principles of feedback and phase relationships in electronic circuit design, making them fundamental components in various electronic systems.This article explains the construction and working of feedback oscillators with detailed description of Wien`s bridge oscillator and phase shift oscillator along with their circuit diagram, basic components and practical application Oscillators are those electronic devices that produce a sinusoidal wave form at their output upon application of dc voltage at their input terminals. Although other types of wave forms can also be obtained from them but the basis wave form that they produce is sinusoidal. There can be different types of oscillators like feedback oscillator and negative feedback oscillator.
Here we will be see how we can classify feedback oscillator along with their working principle. These are the oscillators that involve resistor and capacitor in their circuitry for the purpose of required feedback to the amplifier. These categories can further be classified in to two types that are given as: It is so important type of feedback circuit that it provides a standard as the variable frequency testing circuit in audio frequency range.
The operation of this circuit is very simple. Also it is less complex than LC oscillators. It is actually an audio oscillator that is used in the frequency range of audible range generally generated through speakers. And it is seldom used in testing of those electronic circuits that operate upon audio frequencies. Usually a sinusoidal wave form is generated by this type of oscillator that occurs to be variable both in frequency and amplitude so that it may be adjusted according to the concerned application.
Other than sinusoidal waveform some other wave forms can also be generated with help of them like square wave but it utilizes the same principle for that purpose too. The amplitude generated by them is generally in the range of about 25V and frequency occurs in range of about 20Hz to 20 KHz.
The output impedance of the audio oscillator is in the range of 75 to 600 ohm. The most common oscillators as Wien`s bridge oscillator and phase shift oscillator and both of them apply RC network in their operation. There are some very important features regarding RC oscillators are: It is actually a type of feedback oscillator where the function of the Wien`s bridge is to provide inversion of phase.
There inversion of phase does not mean to shift the phase by 180 degree only but the shift in phase can be by any angle. It is basically an AC bridge such the balance is achieves at the particular frequency of the whole frequency under given range.
Here is a circuit diagram that shows the circuitry set of a Wien`s bridge network. There are capacitors, resistors and an operational amplifier represented by a triangular symbol getting input from the net work formed by passive components. There are some conditions for oscillations to occur one of them is that he phase shift between E1 and E2 should be equal to zero which is possible in one situation when the bridge is made to be balanced.
The frequency of oscillations is given by: Second condition for making oscillations to occur is the product of gain constant of amplifier and constant H should come to be greater than unity. The requirement of the bridge is to provide feedback to the operational amplifier so the value of E2 should remain always greater than one and phase shift between the two i.
e. E1 and E2 remain to be zero. From the discussion so far it has become clear that frequency of oscillation `s` is equal to that of resonance. And Ea does not come to be equal to E1 at any frequency other than resonance frequency. This results in the consequence that the difference of Ea and Eb does come to be in phase with E1. The capacitor that is used in above circuit is of air by variable capacitor which is mounted on the same shaft.
The change is frequency of the bridge is done by means of this capacitor. But this leads to only small variations in frequency while for large variations there exit 🔗 External reference
Related Circuits
The test circuit features a feedback factor of 1/83 utilizing the DA6101Q/6111Q. The input signal is fed through a network comprising resistors R1 and R9, and capacitors C1, C2, and C3, entering the TDA6101Q, which includes three pins for...
Basic reference transistor bias circuit - Mixed Negative feedback The basic reference transistor bias circuit utilizing mixed negative feedback is a fundamental electronic configuration designed to stabilize the operating point of a transistor. This circuit typically employs a combination of...
RC oscillators utilize resistors and capacitors to produce low or audio-frequency signals. Therefore, they are often referred to as audio-frequency (A.F) oscillators. RC oscillators are fundamental circuit designs utilized in various applications for generating periodic waveforms, particularly in the audio...
The circuit oscillates because the transistor shifts the phase of the signal 180 degrees from the base to the collector. Each of the RC networks in the circuit is designed to shift the phase 60 degrees at the frequency...
The circuit is a decay feedback tone control circuit that incorporates anti-attenuation feedback action. Its primary function is to enhance or attenuate bass frequencies, although this distinction can sometimes be challenging to perceive. The analysis utilizes the superposition theorem,...
The circuit is designed exclusively for fundamental crystals, as it lacks mode suppression components. The oscillator transistor Q104 remains in a cutoff state for most of the time, activating only briefly during the peak of the crystal current waveform....