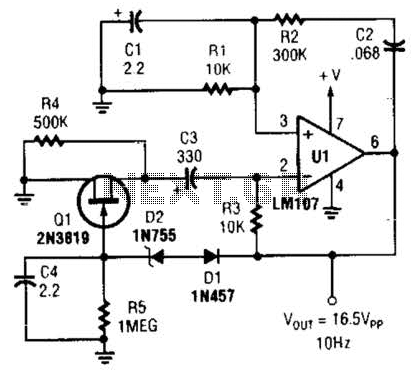
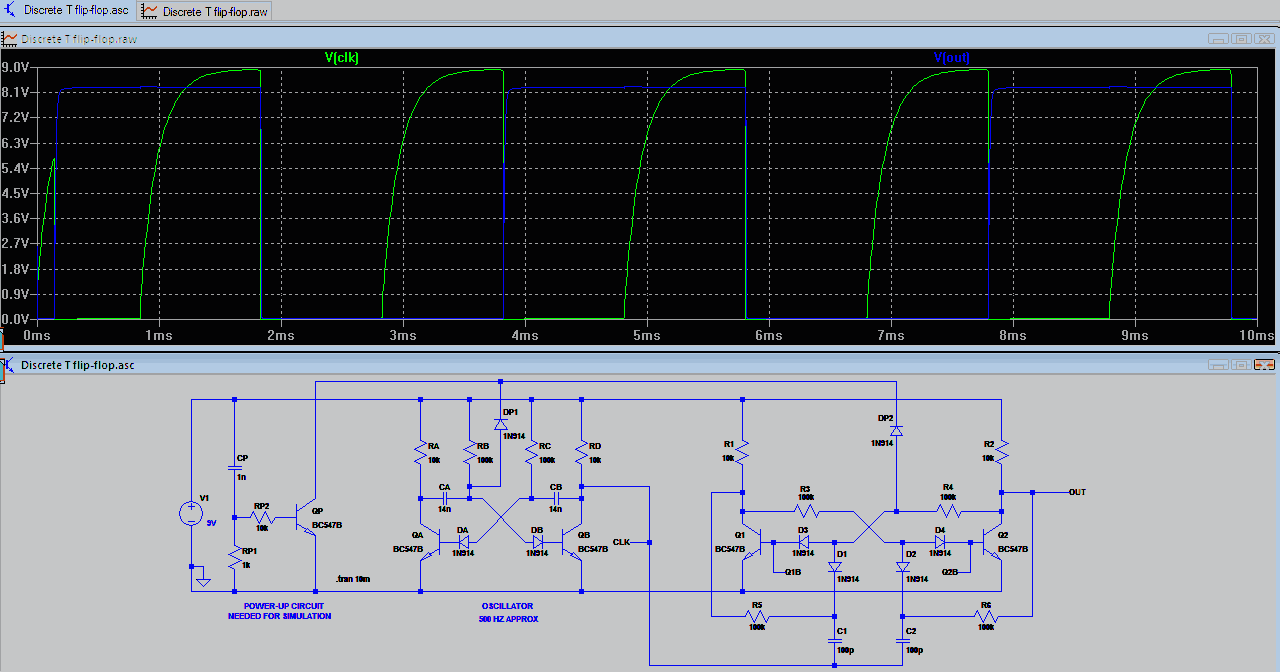
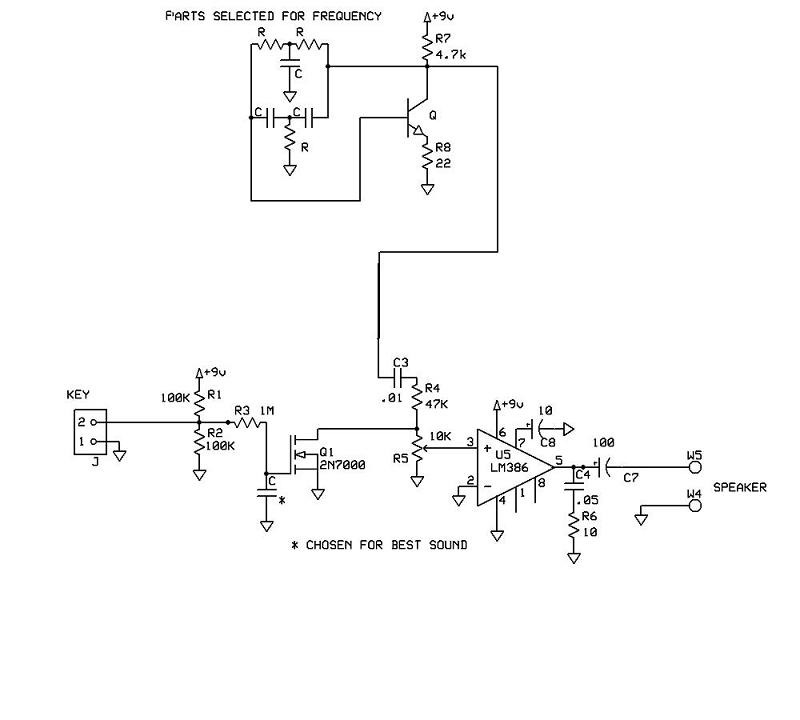
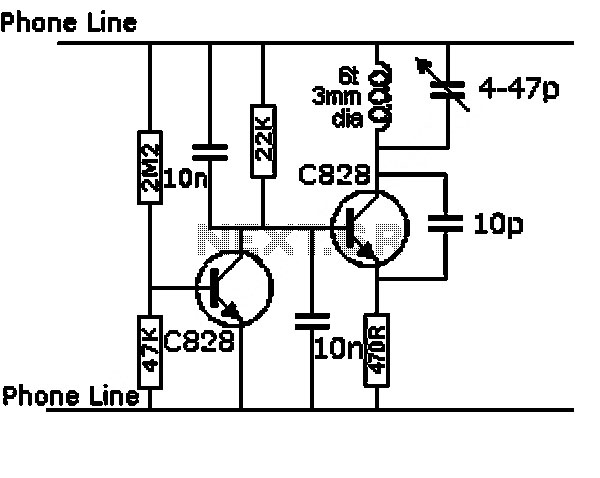
Hartley Oscillator Calculator

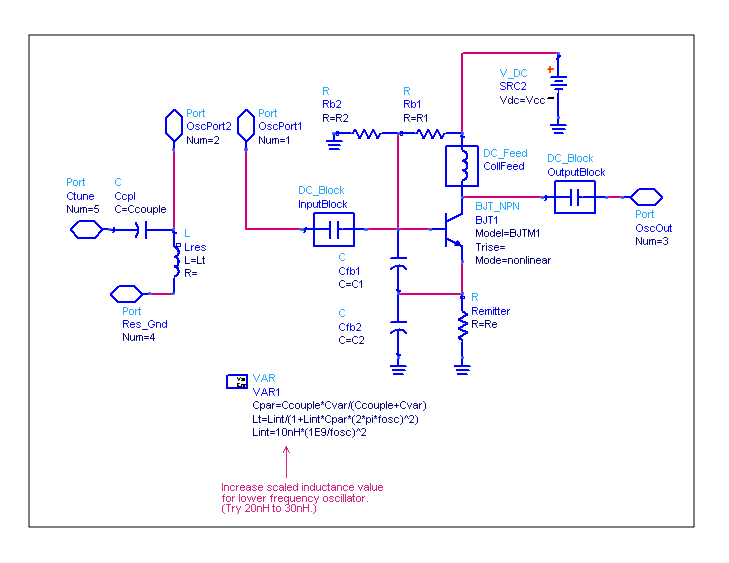
Q is the transistor, L1 and L2 form a resonant circuit, with L2 also serving as a feedback network. The feedback voltage is transmitted to the transistor base through the coupling capacitor Cb. Figure 2 illustrates the communication channel, where the resonant circuit connects three endpoints, each linked to a transistor. This configuration is known as the inductive three-point oscillator circuit, or feedback oscillation circuit inductance. In a high-Q circuit, the oscillation frequency closely matches the resonant frequency of the LC circuit, as described by the relevant formula. The inductance characteristics of the three-point oscillator circuit facilitate easy oscillation initiation, but the output waveform quality is compromised. This is due to the feedback voltage derived from both ends of the inductor, where the inductance exhibits higher impedance at high harmonics, leading to a feedback voltage rich in harmonic components. Consequently, the output waveform also contains a significant number of high harmonics.

The inductive three-point oscillator circuit is a specialized configuration that leverages the characteristics of inductors and capacitors to generate oscillations. The circuit comprises a transistor (Q), two inductors (L1 and L2), and a capacitor (C) that together form a resonant LC circuit. The feedback mechanism is critical for sustaining oscillations; L2 not only participates in the resonant circuit but also acts as a feedback network, providing necessary voltage to the base of the transistor through the coupling capacitor (Cb).

The design allows for the creation of a communication channel, where the resonant circuit connects three distinct endpoints, each associated with a transistor. This arrangement enables efficient signal transmission and amplification, making it suitable for various applications in communication systems.

In terms of performance, the high-Q characteristic of the circuit ensures that the oscillation frequency remains closely aligned with the resonant frequency of the LC circuit. The relationship is defined by the formula governing LC resonant circuits, which indicates the frequency at which the circuit naturally oscillates. However, while the three-point oscillator is adept at initiating oscillations, the output waveform quality can be suboptimal.

This degradation arises from the feedback voltage that is influenced by the inductance at both ends of the inductor. At higher frequencies, the impedance of the inductance increases, which can introduce additional harmonic components into the feedback signal. As a result, the output waveform not only reflects the fundamental frequency but is also populated with high harmonics, which can distort the signal and affect the overall performance of the circuit.

In summary, the inductive three-point oscillator circuit is a complex yet effective design that exemplifies the interplay between inductance, capacitance, and feedback mechanisms in generating oscillations, albeit with certain trade-offs in output waveform fidelity.Q is the transistor, L1, L2, C resonant circuit formed, L2 double as feedback network, through the coupling capacitor Cb will be sent to feedback voltage transistor base. Figure 2 shows the communication channel, resonant circuit with three endpoints and the three most connected transistor, it is known as the inductive three-point oscillator circuit, also known as feedback oscillation circuit inductance.

When a high-Q circuit, the circuit`s oscillation frequency essentially equal to the resonant frequency of LC circuit, the formula is as follows: Inductance characteristics of three-point oscillator circuit is easy to start oscillating, but its output waveform is poor, due to feedback voltage from both ends of the inductor, while the inductance of the high harmonics of the impedance of a larger, and thus contains the feedback voltage more harmonic components, therefore, the output waveform also contains more high harmonics. 🔗 External reference