potential difference between point x and point y

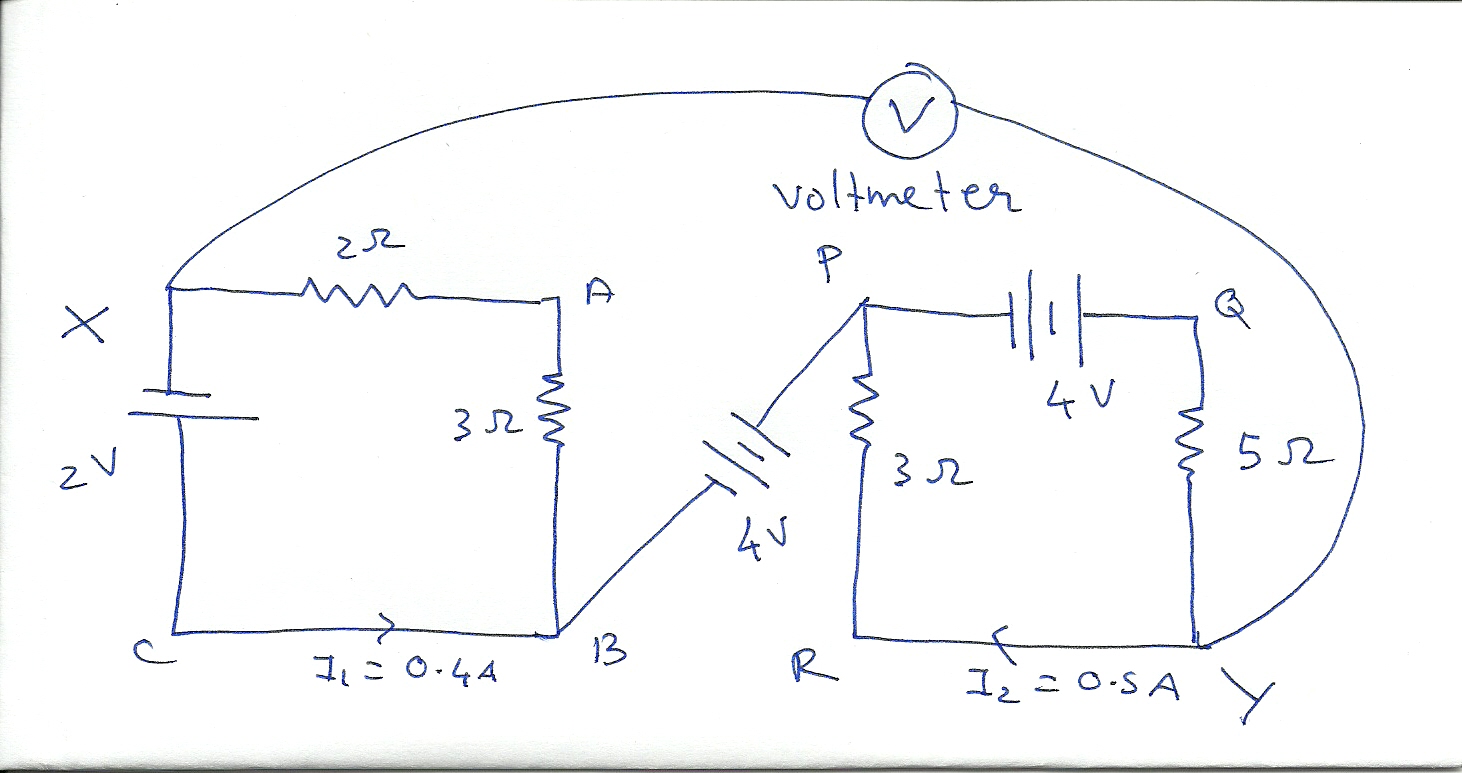
The current in both loops was determined using Kirchhoff's Voltage Law. However, there is confusion regarding the correct method to find the potential drop between the two loops. It is suggested to insert two additional points, A and B, at both ends of the battery (located at the bottom right of the left square and the top left of the right square). The calculation of the potential difference between points X and A, A and B, and finally B and Y is required. The potential drop between points X and Y needs clarification, especially considering the presence of a 4V battery in the middle through which no current flows. The potential across the battery is 4V, but there is no complete circuit between nodes A and B, resulting in no current flow.

In this scenario, Kirchhoff's Voltage Law (KVL) is applied to analyze the circuit, which consists of two loops and a 4V battery. The voltage law states that the sum of the potential differences (voltage) around any closed loop in a circuit must equal zero. To find the potential drop between the specified points, it is essential to define the reference points clearly.

To calculate the potential difference between points X and Y, first, identify the voltage across the battery. Since the battery has a voltage of 4V and no current flows through it, this voltage remains constant across its terminals. When analyzing the circuit, the potential at point X can be considered as a reference point, typically set to 0V. As one moves from point X to point A, the voltage will increase by the battery's voltage, resulting in a potential at point A of +4V.

Next, to find the potential at point B, it is important to recognize that if there is no current flowing between nodes A and B, the voltage at point B will also be +4V, as there is no voltage drop across an open circuit. Consequently, the potential difference between points A and B is 0V.

Finally, to determine the potential at point Y, one must consider the entire loop. If point Y is connected to the battery and no additional resistances or components are present, it will also be at +4V. Therefore, the potential difference between points B and Y will also be 0V.

In summary, the potential differences can be calculated as follows:
- V(X to A) = 4V
- V(A to B) = 0V
- V(B to Y) = 0V

The overall potential drop between points X and Y can be summarized as being equal to the voltage of the battery, which is 4V, due to the direct connection through the battery. This analysis provides a comprehensive understanding of how to approach the calculation of potential drops in circuits involving multiple loops and components.found the current in both the loops using Kirchhoff`s Voltage law but then I`m confused on the proper method to find the potential drop between the two loops. I suggest you insert two extra points A and B on both ends of the battery (on the bottom right of the left square and the top left of the right square).

Can you calculate the potential difference between X and A, A and B, and finally B and Y Gerben Oct 21 `11 at 12:46 @DavidZaslavsky I found the current in both the loops using Kirchhoff`s Voltage law but then I`m confused on the proper method to find the potential drop between the points X and Y may be can you explain me the procedure as well as find the potential drop between X and Y since there is a 4V battery in middle through which no current flows I wonder how to calculate the potential drop between X and Y+ Praveen Gowda I V Oct 21 `11 at 14:59 @PraveenGowdaIV - There is no complete circuit between nodes A and B, so no current flows. The potential across the battery is. the potential across the battery; 4V. Kevin Vermeer Oct 21 `11 at 15:33 🔗 External reference