square wave 2 sine wave convertion
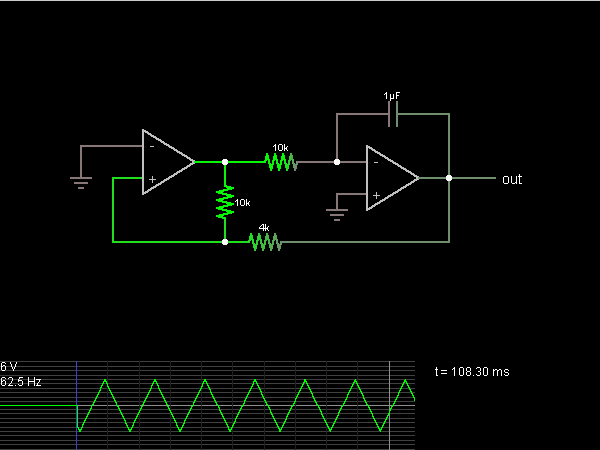
A TTL square wave needs to be converted into a sine wave, with a frequency range of 4Hz to 60Hz. One method to achieve this is by filtering the square wave using a high-order filter. However, if the frequency varies, a tracking filter with a center frequency that adjusts according to the input frequency is required, which is complex to implement. An alternative approach involves passing the square wave through two integrators in series. The first integrator produces a triangular wave, while the second generates a sine wave. A challenge with this method is that the output amplitude is inversely proportional to the square of the frequency, necessitating an Automatic Gain Control (AGC) circuit to maintain a constant amplitude. Given the specified frequency range, the amplitude could vary significantly by a factor of 225 or 47dB. A switched-capacitor Butterworth low-pass filter integrated circuit (IC) operates with a clock frequency that is 100 times the cutoff frequency. This clock can be derived from the Voltage-Controlled Oscillator (VCO) of a phase-locked loop (PLL) IC, with a digital divider generating the fundamental frequencies. The clock frequency must be significantly higher than the output frequency, and the frequency is specified digitally, indicating that this is not a direct conversion. The MAX7400-7407 datasheet presents some confusion, as it contains unfamiliar information. It is understood that the output frequency equals Fclk/100. Adjustments have been made to the circuit to reduce the workload on the filter, although attenuation is more pronounced at higher frequencies compared to lower frequencies. Incorporating an AGC amplifier after the filtering stage may stabilize the output amplitude.
To convert a TTL square wave into a sine wave effectively, a multi-stage approach is recommended. The initial step involves using a high-order low-pass filter to suppress the higher harmonics of the square wave. This could be achieved with a switched-capacitor Butterworth low-pass filter IC. The operation of this filter should be synchronized with a clock frequency that is 100 times greater than the desired cutoff frequency, which ensures that the filter can adequately smooth the square wave.
In cases where the input frequency varies, implementing a tracking filter is crucial. This filter's center frequency must dynamically adjust to match the input frequency, which can be accomplished using a phase-locked loop (PLL) configuration. The PLL can utilize a voltage-controlled oscillator (VCO) to generate the required clock signal, while a digital divider can produce the corresponding fundamental frequencies.
Following the initial filtering, the square wave should be passed through two integrators in series. The first integrator will transform the square wave into a triangular wave, which is a necessary step before converting it into a sine wave. The second integrator will then produce the sine wave output. However, it is essential to address the amplitude variation issue; as the frequency increases, the output amplitude decreases inversely with the square of the frequency.
To maintain a consistent output amplitude across the frequency range of 4Hz to 60Hz, an AGC circuit should be integrated into the design. This circuit will automatically adjust the gain based on the output signal level, ensuring that the amplitude remains stable despite variations in frequency.
The output from this configuration will provide a clean sine wave signal suitable for low-frequency applications. It is important to ensure that all components are appropriately rated for the frequency range and that the circuit is designed to minimize noise and distortion, thereby producing a high-quality sine wave output.I would like to convert a TTL square wave into sine wave. The frequency range of the square wave is: 4Hz-60Hz (yes its those evil low frequency experiments that I plant to take over the world with One approach is to filter the square wave with a high order filter. But if the frequency varies then you need a tracking filter whose center frequency v aries with the input frequency. That`s not trivial to do. Another technique is to run the square-wave through two integrators in series. The first integrator generates a triangular wave and the second generates a sine wave. The problem is that the output amplitude is inversely proportional to the square of the frequency so you need some sort of AGC circuit to maintain a constant amplitude. For a frequency range of 4Hz-60Hz the amplitude would vary by a factor of 225 or 47dB. A switched-capacitor Butterworth lowpass filter IC uses a clock that is 100 times the cutoff frequency.
The clock can be the VCO of a phase-locked-loop IC and a digital divider produces the fundamental frequencies. You need to clock them many times faster than the output frequency and you tell them the frequency digitally, so it is not a direct conversion, but that might help.
A switched-capacitor Butterworth lowpass filter IC uses a clock that is 100 times the cutoff frequency. The clock can be the VCO of a phase-locked-loop IC and a digital divider produces the fundamental frequencies.
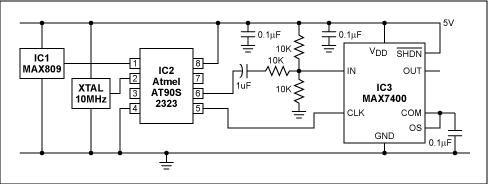
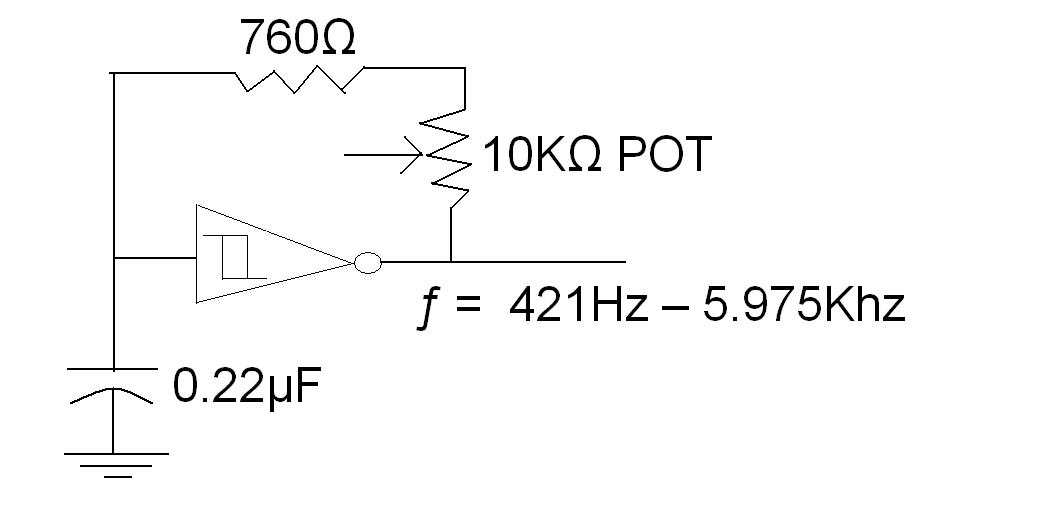
I tried reading the datasheet for MAX7400-7407 but I am confused. Most of the information presented on the datasheet is new to me. From what I understood, the output frequency will = Fclk/100. So I made some adjustments to my circuit below: This would make it less work for the filter. The problem is that the attentuation is greater at higher frequencies than lower frequencies. If you put it through an AGC amplifier after it`s been through the filter then you could hopefully stablise the output amplitude enough. 🔗 External reference
To convert a TTL square wave into a sine wave effectively, a multi-stage approach is recommended. The initial step involves using a high-order low-pass filter to suppress the higher harmonics of the square wave. This could be achieved with a switched-capacitor Butterworth low-pass filter IC. The operation of this filter should be synchronized with a clock frequency that is 100 times greater than the desired cutoff frequency, which ensures that the filter can adequately smooth the square wave.
In cases where the input frequency varies, implementing a tracking filter is crucial. This filter's center frequency must dynamically adjust to match the input frequency, which can be accomplished using a phase-locked loop (PLL) configuration. The PLL can utilize a voltage-controlled oscillator (VCO) to generate the required clock signal, while a digital divider can produce the corresponding fundamental frequencies.
Following the initial filtering, the square wave should be passed through two integrators in series. The first integrator will transform the square wave into a triangular wave, which is a necessary step before converting it into a sine wave. The second integrator will then produce the sine wave output. However, it is essential to address the amplitude variation issue; as the frequency increases, the output amplitude decreases inversely with the square of the frequency.
To maintain a consistent output amplitude across the frequency range of 4Hz to 60Hz, an AGC circuit should be integrated into the design. This circuit will automatically adjust the gain based on the output signal level, ensuring that the amplitude remains stable despite variations in frequency.
The output from this configuration will provide a clean sine wave signal suitable for low-frequency applications. It is important to ensure that all components are appropriately rated for the frequency range and that the circuit is designed to minimize noise and distortion, thereby producing a high-quality sine wave output.I would like to convert a TTL square wave into sine wave. The frequency range of the square wave is: 4Hz-60Hz (yes its those evil low frequency experiments that I plant to take over the world with One approach is to filter the square wave with a high order filter. But if the frequency varies then you need a tracking filter whose center frequency v aries with the input frequency. That`s not trivial to do. Another technique is to run the square-wave through two integrators in series. The first integrator generates a triangular wave and the second generates a sine wave. The problem is that the output amplitude is inversely proportional to the square of the frequency so you need some sort of AGC circuit to maintain a constant amplitude. For a frequency range of 4Hz-60Hz the amplitude would vary by a factor of 225 or 47dB. A switched-capacitor Butterworth lowpass filter IC uses a clock that is 100 times the cutoff frequency.
The clock can be the VCO of a phase-locked-loop IC and a digital divider produces the fundamental frequencies. You need to clock them many times faster than the output frequency and you tell them the frequency digitally, so it is not a direct conversion, but that might help.
A switched-capacitor Butterworth lowpass filter IC uses a clock that is 100 times the cutoff frequency. The clock can be the VCO of a phase-locked-loop IC and a digital divider produces the fundamental frequencies.
I tried reading the datasheet for MAX7400-7407 but I am confused. Most of the information presented on the datasheet is new to me. From what I understood, the output frequency will = Fclk/100. So I made some adjustments to my circuit below: This would make it less work for the filter. The problem is that the attentuation is greater at higher frequencies than lower frequencies. If you put it through an AGC amplifier after it`s been through the filter then you could hopefully stablise the output amplitude enough. 🔗 External reference