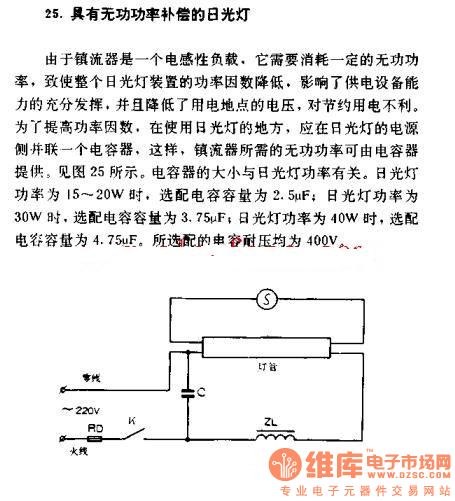
Johnson digital counter circuit diagram using D flip flop 7474 (3 bit/4 bit) with animation/ simulation

The Johnson digital counter, also known as the Twisted Ring Counter, is a synchronous shift register that incorporates feedback from the inverted output (Q`) of the last flip-flop. The Q` output of the final flip-flop is connected back to the input D of the first flip-flop. This inversion of Q before being fed back to input D enables the counter to count in a unique manner. The article also includes an animation/simulation of this Johnson counter circuit, which can be utilized to create simple dancing LED effects using this synchronous Johnson digital counter. A significant advantage of this counter type is that it requires only half the number of flip-flops compared to a standard ring counter to represent a larger number of states. An n-stage Johnson counter generates a sequence of 2n different states, functioning as a Mod 2n counter, while an n-stage ring counter produces only n states, acting as a Mod n counter. The circuit diagram illustrates a 3-bit Johnson counter using 7474 D flip-flops. This circuit can be easily extended to 4 bits, 5 bits, and beyond by adding additional flip-flops after the third flip-flop. Initially, a logic high (1) is applied to the input of the first flip-flop. During the first clock pulse, this logic high is transferred to the output of the first flip-flop, resulting in a total output of 100. With the logic high present at the inputs of the first and second flip-flops, after the second clock pulse, these inputs appear at the outputs of the first and second flip-flops, yielding a total output of 110. During this state (111), the inverted output (Q`) becomes logic low (0). This logic low is then fed back to the first flip-flop, causing a circulation through the flip-flops that results in the outputs transitioning through 011, 001, and finally 000.

The Johnson counter is characterized by its unique counting mechanism, which is facilitated by the feedback loop that introduces a delayed inversion of the last flip-flop's output. This allows the counter to produce twice the number of states compared to a traditional ring counter. The circuit typically consists of a series of D flip-flops configured in a chain, where the output of one flip-flop serves as the input for the next.

In practical implementations, the 7474 D flip-flop is commonly used due to its reliability and availability. Each flip-flop in the Johnson counter is clocked simultaneously, ensuring synchronous operation. The initial state of the counter can be set by applying a logic high to the first flip-flop, which will propagate through the chain upon receiving clock pulses. The counter's output can be monitored at various stages, allowing for the observation of the counting sequence as it progresses through its states.

To extend the Johnson counter beyond three bits, additional D flip-flops can be added in series, with the final flip-flop's Q` output still being fed back to the first flip-flop's D input. This modularity makes the Johnson counter a versatile choice for various digital applications, including LED control, frequency division, and other tasks requiring a reliable sequence of states. The simplicity of the circuit, combined with its efficient use of flip-flops, makes it an attractive option for digital design.The Johnson digital counter or Twisted Ring Counteris a synchronous shift register with feedback from the inverted output (Q`) of the last flip-flop. Q` of the last flip flop is connected back to the input D of the first flip-flop. This inversion of Q before it is fed back to input D causes the counter to count  in a special way. Animation/ simu lation of this Johnson counter circuit is also given in this article. You can create simple dancing LED effects using this synchronous Johnson digital counter. The main benefit of this type of counter is that it only needs half the number of flip flops compared to that of standard ring counter to represent many states. So an n-stage Johnson counter givies a sequence of 2n different states and can therefore be treated as a Mod 2n counter  whereas an n-stage ring counter has only n states that is Mod n counter .

Above circuit diagram represents a 3 bit Johnson counter using 7474 D flip flop. You can easily extent this circuit upto 4 bit, 5 bit, etc. by adding flip flops after the 3rd flips flop. This logic 1 is appears at the input of 1st flip flop. During the first clock pulse this logic 1 is transferred to the output of 1st flip flop. Thus the total output of Johnson counter is 100. Then input of 1st and 2nd flip flop is logic 1 and after the second clock pulse these inputs appear at the outputs of 1st and 2nd flip flop. So the total output is 110. During this state (111) the time inverted output (Q`) is logic 0. This 0 is fed to the 1st flip flop. Then the 0 will circulate through the flip flops as 011, 001, 000. 🔗 External reference