Phase shift oscillator circuit

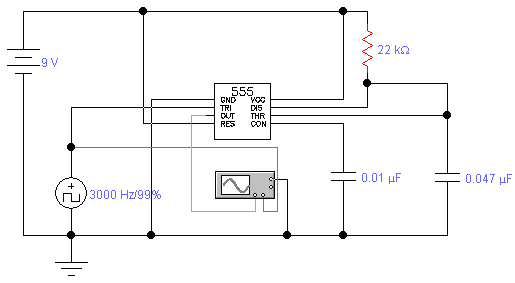
The standard assumption is that the phase shift sections operate independently. According to the equation provided, the loop phase shift reaches -180 degrees when the phase shift of each section is 60 degrees. This condition is met when ω = 2πf = 1.732/RC, as the tangent of 60 degrees equals 1.732. At this point, the magnitude of β is (1/2)^3. Consequently, for the system gain to equal one, the gain, A, must be set to 8. Additionally, the theoretical gain of the operational amplifier is 8, while the practical gain required to initiate oscillation is 32.4, and the practical gain necessary to maintain oscillation is 31.6. The theoretical frequency is calculated to be 2.76 kHz, whereas the practical frequency is observed at 3.78 kHz. The primary reason for this discrepancy is that the RC sections are not buffered, which causes them to load each other. Furthermore, the tolerance of component values can lead to variations in the results. Nevertheless, there is a significant reduction in distortion when compared to the Wien bridge oscillator.

The described circuit involves an operational amplifier configured for oscillation, specifically utilizing phase shift networks. The architecture typically consists of multiple RC (resistor-capacitor) sections that contribute to the overall phase shift necessary for sustained oscillation. The assumption of independence among these sections is crucial; if they were to interact, the phase shift would not achieve the required -180 degrees at the designated frequency.

In this configuration, the operational amplifier's gain must be precisely calculated to ensure that it meets the necessary conditions for oscillation. The theoretical gain of 8 is derived from the requirement that the total feedback loop gain equals one at the point of oscillation initiation. However, practical applications often necessitate a higher gain of approximately 32.4 to overcome losses and achieve stable oscillation.

The frequency of oscillation is determined by the values of the resistors and capacitors in the RC sections. The theoretical frequency of 2.76 kHz is based on ideal component values, while the practical frequency of 3.78 kHz reflects real-world conditions, including component tolerances and loading effects. The lack of buffering in the RC sections leads to loading effects that can alter the expected phase shift and gain, resulting in discrepancies between theoretical and practical outcomes.

This circuit design demonstrates improved performance characteristics, particularly in terms of distortion, when compared to traditional Wien bridge oscillators. The phase shift network's design and the operational amplifier's configuration play a critical role in achieving the desired oscillation characteristics while minimizing distortion, making it a valuable design for various electronic applications.The normal assumption is that the phase shift sections are independent of each other. Then using above Equation the loop phase shift is –1800, when the phase shift of each section is 600. This occurs when ω=2πf = 1.732/RC because the tangent of 600 = 1.732. The magnitude of β at this point is (1/2)3. So the gain, A, must be equal to 8 for the system gain to be equal to one. Therefore theoretical gain of op-amp = 8 The practical gain to start an oscillation = 32.4 The practical gain to keep oscillation = 31.6 Theoretical frequency = 2.76 Khz Practical frequency = 3.78 Khz The main reason for this is RC sections are not buffered. That is they load each other. Also the tolerance of the values of components can vary the results. But still there is a remarkable reduction in distortion comparing to the wein bridge oscillator. 🔗 External reference