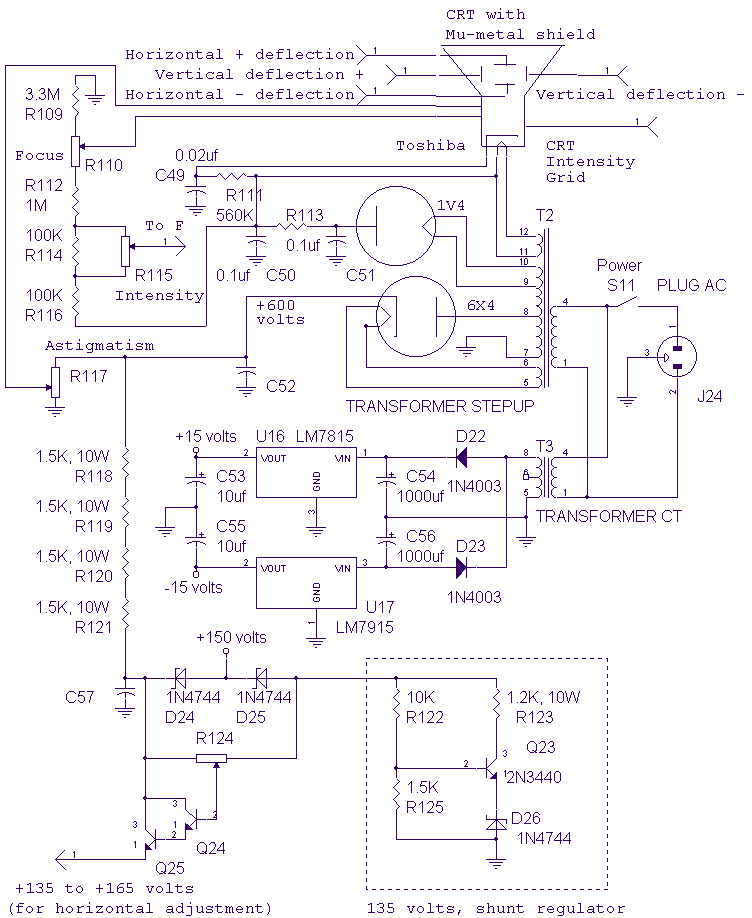
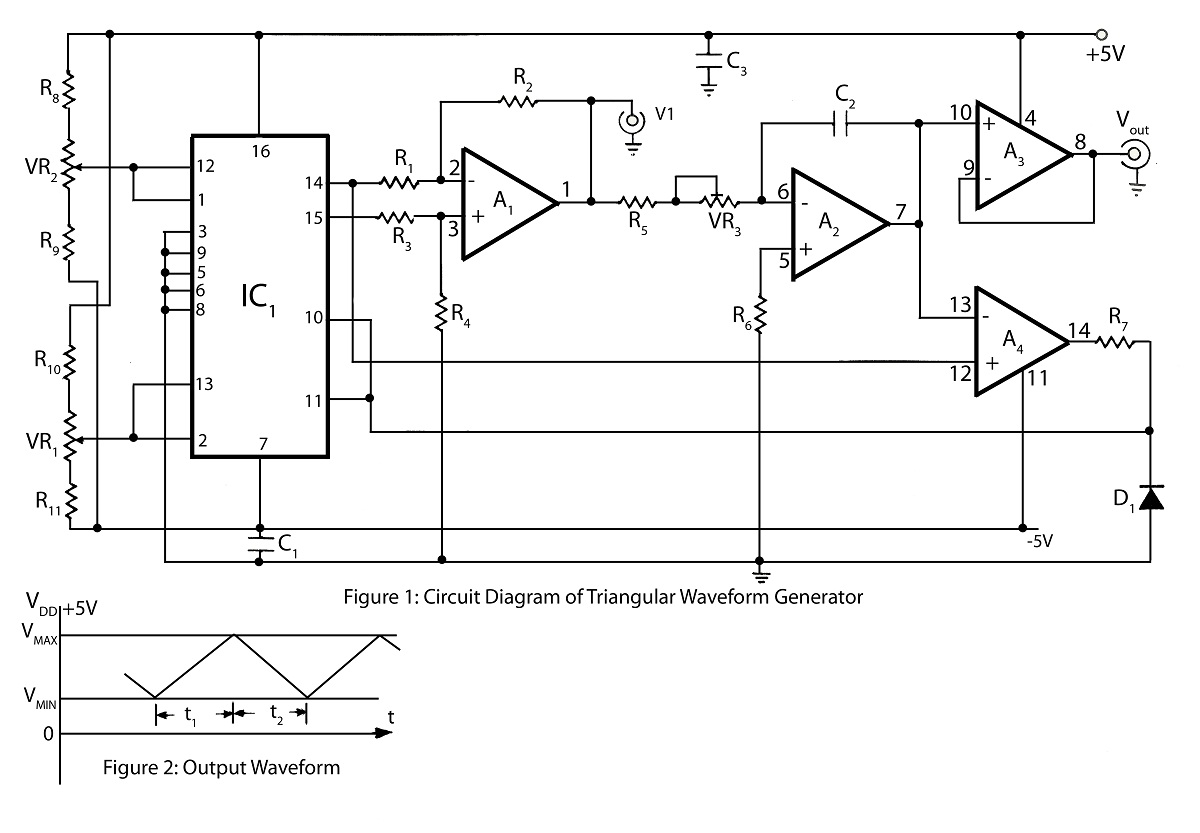
Single Supply Function Generator

The ratio R1/R2 determines the amplitude of the triangle wave in relation to the square-wave output. The frequency of oscillation for both waveforms can be calculated using the equation: fo = 1/(4R3C1) * (R2/R1).

In this circuit, R1 and R2 play a crucial role in shaping the amplitude of the triangle wave generated. The relationship between these resistors dictates how high or low the triangle wave will oscillate, directly influencing the output characteristics when compared to the square wave. The triangle wave's amplitude is critical for applications that require precise waveform characteristics, such as in signal processing or modulation techniques.

The frequency of oscillation is determined by the equation provided, where R3 and C1 are additional components that help define the timing characteristics of the circuit. R3 is a resistor that, in conjunction with the capacitor C1, sets the time constant for the charging and discharging cycles that produce the oscillation. The factor of 4 in the denominator indicates that the frequency is inversely proportional to the product of R3 and C1, meaning that increasing either component will decrease the frequency of oscillation.

This configuration allows for flexibility in tuning the circuit to achieve desired waveform frequencies and amplitudes. The ratio of R2 to R1 allows for further fine-tuning of the triangle wave's amplitude, which can be essential in applications such as waveform generation, signal modulation, and audio synthesis. By adjusting these resistors, one can achieve a wide range of output characteristics suitable for various electronic applications.

Overall, the interplay between R1, R2, R3, and C1 is fundamental in designing circuits that require precise waveform generation, making this configuration valuable in both educational and practical electronic engineering contexts.The ratio R1/R2 sets the amplitude of the triangle wave, as referenced to the square-wave output. For both waveforms, the frequency of oscillation can be determined by the equation: fo= 1/4R3C1 * R2/R1 🔗 External reference